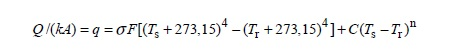Puissance émise

Oxa-libre
#1

Bonjour à tous,

Je me pose une question concernant la puissance réelle émise par un poêle de masse, et j’aimerais bénéficier de vos connaissances à ce sujet. Voici les données que j’ai recueillies :

  • La déperdition thermique de ma maison est de 2,8 kW environ.
  • J’ai choisi un poêle de masse Oxa-libre 6 kW - 2T300.
  • Dans ma configuration, la surface d’échange du poêle comprend la face avant et les deux demi-côtés, soit environ 2,8 m². En effet, la face arrière est « encastrée » dans un mur.

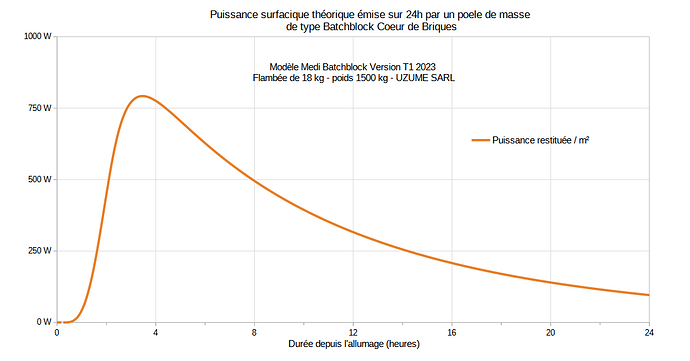
J’ai également entendu dire quelque part que la puissance émise par un poêle de masse est d’environ 400 W/m². J’aimerais donc savoir si cette estimation est valable dans mon cas, et quelle serait la puissance réelle émise par mon poêle de masse en tenant compte de ces informations.

Si la puissance est bien de 400W/m², mon poêle peut retransmettre en peu moins de 1.1kW.
La chaleur émise par la face arrière peut surement être récupérer par un système groupe air chaud, quelqu’un à déjà mis ça en place ?

Je vous remercie d’avance pour vos réponses

#2

Bonjour @Flo , c’est une approche intéressante !

La puissance surfacique émise par un poele de masse ne peut pas etre constante, elle dépend énormément de sa conception et du nombre de flambée qu’il peut gérer par jour : de manière générale, plus un poele de masse est lourd et grand, moins la puissance surfacique sera élevée.

C’est pour ca qu’on se base plutot sur la puissance « globale » émise par le poele pour le dimensionner.

Pour le calcul de la puissance surfacique :

Sur l’oxalibre de 6kW, la puissance moyenne sur 24h est de 3.8 kW (ca dépend carrément de comment on définit ce terme, voir Dimensionnement fumisterie poele OXALIS et pour l’exemple, je pars sur 3 flambées/jour) mais 9kg de bois × 4,1kWh/kg ×3 flambées/ jour × 83% de rendement global / 24h = 3.8 kW

Cette chaleur n’est pas vraiment la chaleur émise, c’est plutot la chaleur produite et récupérée par le poele. Et je suppose pour le calcul que le poele a le temps de diffuser la chaleur des 3 flambées en 24h.

Pour arriver à la puissance émise, il faut enlever la chaleur qui part dans la cheminée après la fin de la flambée… mais je n’ai pas de valeur expérientale dessus pour l’instant et ca dépend de si il y a un clapet d’obstruction ou pas.

Du coup si on dit que ces 3.8 kW ne sont diffusés que dans la pièce et par la partie avant du poele, on arrive à 1360 W/m2.

#3

Bonjour @yasin , il y a quelque chose que je n’arrive pas à comprendre…
Comment un matériaux peut avoir peut voir se puissance surfacique augmenter selon des facteurs plus ou moins externe? En effet, il me semble que la chaleur émise par le poêle est répartie plus ou moins uniformément sur l’enveloppe (Peut-être un peu moins en bas qu’en haut).

Donc un poêle normalement disposé, avec toutes ses faces prêtes à émettre la chaleur accumulée ce verra avec une chaleur diffusée à 530 W/m2 (3,8kW/7m2).

Pour émettre à 1360 W/m2, ne fraudait-il pas une surface avec une température nettement supérieure à la configuration dites « normale » ?

#4

Bonjour @Flo j’avais repris ton hypothèse que la chaleur ne serait pas diffusée par les faces encastrées dans le mur, mais c’est sur qu’il y aura une partie de la chaleur qui se diffusera par ces faces.

Par contre, je pense bien qu’il y aura moins de chaleur qui ira qui se diffusera par ces faces. C’est comme sur un poele avec un habillage très épais : la température de surface est plus faible, donc la puissance émise est plus faible, donc il y a moins d’énergie qui traverse ce mur.

Ca veut dire que l’énergie qui sera émise par les murs non encastrés sera plus importante. Donc la température de surface de ces parois sera aussi plus importante. Tu obtiendrais un résultat encore plus prononcé en isolant les faces arrières du poele : la chaleur doit bien sortir quelque part.

La température liée à la puissance surfacique se calcule à partir de la loi de stephan-boltzmann :

DT = (P / (ε * σ))^(1/4)-273

avec P la puissance surfacique en W/m2
ε l’émissivité = 0.91
σ = 5,670 10-8 W.m-².K-4 la constante de stephan-boltzmann
DT la température différencielle entre la pièce et la surface du poele en °C

Si P = 1360 W/m2, alors DT = 130°C (les parois du poele sont 130°C plus chaudes que les parois de la pièce)
Si P = 530 W/m2, alors DT = 45°C

Sur un poele uzume (le medi batchblock) ca donne :

2023-07-19_puissance_surfacique_theorique_emise_medi_batchblock_cdbr
2023-07-19_puissance_surfacique_theorique_emise_medi_batchblock_cdbr1086×569 27.5 KB

On atteint un pic à environ 800W/m2, donc au moment du pic les parois du poele sont en moyenne 80°C plus chaudes que les parois de la pièce

edit : avec la bonne formule (celle d’ @edufas) les parois du poele sont en moyenne 72°C plus chaudes que les parois de la pièce au moment du pic.

#5

P n’est pas la puissance surfacique mais la puissance surfacique rayonnée. Pour obtenir la puissance surfacique totale il faut ajouter la contribution de la convection qui est loin d’être négligeable, une formule appliquée simple (sans avoir a faire de transport) : Convective Heat Transfer

DD

#6

Merci @andre ! Tu as raison la loi de stephan-boltzmann n’est valable que dans le vide où il n’y a pas de convection…

Comment tu trouves le coefficient pour brique/air hc = convective heat transfer coefficient of the process (W/(m2oC, Btu/(ft2 h oF)) ?

Parce qu’ils donnent une fourchette super large : * Free Convection - air, gases and dry vapors : 0.5 - 1000 (W/(m2K))

#7

Salut Yasin,

Désolé, les math ne sont pas mon talent, ça à sauté ma génération :wink:
Je laisse volontiers à des personnes compétents.

Je suis souvent modestement sceptique au sujet de comment les chiffres sont obtenues (car les mesures thermiques sont très loin d’être simple),
mais après on fait ‹ ce qu’on peut avec ce qu’on a ›. Tant qu’on est transparent.

Ce que j’ai conclu pour le moment c’est plus qu’une surface est chaude, plus que le part de convection augmente.
Je ne sais pas citer une source, mais ayant vécu avec un poêle à bois en métal ainsi que des pdm, la différence de temp de (et donc humidité dans) l’air saute aux yeux.
Il serais utile d’avoir une graphique qui le montre.

1 « J'aime »
#8

@yasin

c’est marqué un peu plus bas.

tu peux lire des livres spécialisés sur :
transfert de chaleur
mécanique des fluides et modèles de turbulences

DD

#9

La formule donnée en bas de page n’est malheureusement pas valable ici car les vitesses de l’air sont inférieures à 2 m/s.

Je suis quasiment sûr qu’ @edufas a trouvé cette valeur parce que j’ai une feuille de calcul en espagnol qui doit provenir de lui. :grin:

@edufas , est-ce que tu connais la valeur de ce coefficient pour les parois verticales en briques ? Comment l’as tu calculée ?

#10

En fait @edufas je viens de trouver le document que tu m’avais envoyé avec cette même formule !
image

Ainsi que les valeurs des coefficients nécessaires pour le calcul :

σ 5.67E-08 w/m-2K-4
F 0.80
Ts ºC (superficial)
Tr 20 ºC (ambiente)
C 1.2 w/m-2K-n
n 1.36

L’ensemble provient de la norme EN15250.

J’ai fait une courbe à partir de l’équation d’ @edufas

2023-07-19_puissance_surfacique_emise_poele_de_masse_fonction_temperature_paroi_uzume
2023-07-19_puissance_surfacique_emise_poele_de_masse_fonction_temperature_paroi_uzume906×540 28.2 KB

Donc 1360 W/m2 ca correspond à une température différentielle de surface de 105°C
et 530 W/m2 ca correspond à une température différentielle de surface de 55°C. :grin:

#11

Encore une fois, je pense que le traducteur ne me permet peut-être pas de m’exprimer clairement avec vous, désolé. J’espère que j’ai bien compris.

Si vous regardez attentivement la formule de la EN15250, il y a deux termes qui s’ajoutent l’un à l’autre :

  • la partie de la chaleur fournie par rayonnement (loi de Stefan Bolftmann).
  • La seconde partie de la formule est la chaleur fournie par convection.

La EN15250 recommande d’utiliser les constantes de convection C=1,2 (w/m2ºC) et l’exposant n=1,36 (pour les flux turbulents). Elle recommande également comme approximation la valeur de F =0,8 (en fonction de l’émissivité des parois).

Cette formule donne alors la somme de q= rayonnement + convection.
La seule chose est que la température doit être calculée comme la différence de température moyenne pondérée entre les différentes surfaces.

@andre Merci pour le lien que vous envoyez, j’ai regardé le contenu et il est très bon…

Otra vez creo que quizas el traductor no me permite hablar claramente con vosotros, lo siento. Espero que se entienda.

Si te fijas bien en la formula que viene en la UNE 15250 , hay dos terminos que se suman :

  • la parte de entrega de calor por radiacion (ley Stefan bolftmann)
  • la segunda parte de la formula es el calor entregado por conveccion

La propia UNE 15250 te recomienda usar las constantes de convección C=1.2 (w/m2ºC) y el exponente n=1.36 (para flujo turbulento). Tambien te recomienda como aproximacion el valor de F =0.8 (depende de la emisividad de las paredes)

Esa formula entonces ya te da la suma de q= radiacion + conveccion
Lo unico que la temperatura hay que calcular la diferencia temperatura media ponderada entre las diferentes superficies

@andre gracias por el enlace que mandas , estaba viendo el contenido y es muy bueno…

1 « J'aime »
#12

Merci à tous pour vos éclaircissements, je vais regarder plus en détails pour voir si je comprends tout ça :slight_smile: